Topics on Potential Energy
Negative sign on Gravitational but not electric potential energy
The simplified gravitational potential energy is $U_G=mgh$ with no negative sign. The full versions of both gravity and electric are $$ U_G=-G\frac{Mm}{r} $$ $$ U_E=k\frac{Qq}{r} $$ where we see that $U_G$ has a negative sign but U_E does not. Why is this?
The reason is because gravity is always attractive but charges can either repel or attract.
Under no other influence, objects want to go from high $U$ to low $U$. Two objects in space a distance $r=5$ away will have $U_G\sim-\frac{1}{5}$. In order to reduce $U_G$, it must become more negative and so $r$ must decrease to maybe $r=2$ or even $r=0.5$ so the fraction becomes a more negative number.
The negative sign must be there because mass is always positive and the force is always attractive. For electric, if the charges are both positive, they repel. And we must therefore have lower $U_E$ exist at greater separation between the charges, so they move away and $r$ increases. Just the opposite situation as for $U_G$.
If the charges are opposite in sign, then the product is negative, a negative sign results, we have attraction and the result is similar to $U_G$.
Potential and Force as Negative Gradient
Both electric and gravity forces are the negative gradient of their potential energies.
Since both are conservative forces, they can be represented as the gradient of a scalar potential, $\phi_G$ and $\phi_E$. Then we have that $$ \vect{F}_G=\nabla \phi_G $$ and $$ \vect{F}_E=\nabla \phi_E $$ But we define potential energy as the negative of this potential so that $$ U_G=-\phi_G $$ and $$ U_E=-\phi_E $$
Making this substitution in the force equations, we get $$ \vect{F}_G=-\nabla U_G $$ and $$ \vect{F}_E=-\nabla U_E $$
Don't mix up potentials
The potential $\phi$ used above for the scalar potential of the forces is not the electric potential. The electric potential is related to the electric field by
$$ \vect{E}=-\nabla\varphi $$So the electric field is the negative gradient of the electric potential. A nice similarity between the forces and their own potentials.
From this, combined with the relaitionship between force and electric field of $\vect{F}_E=q\vect{E}$, we have that
$$ \phi=-q\varphi $$as the relationship between the force potential and the electric potential, which is just "the volts."
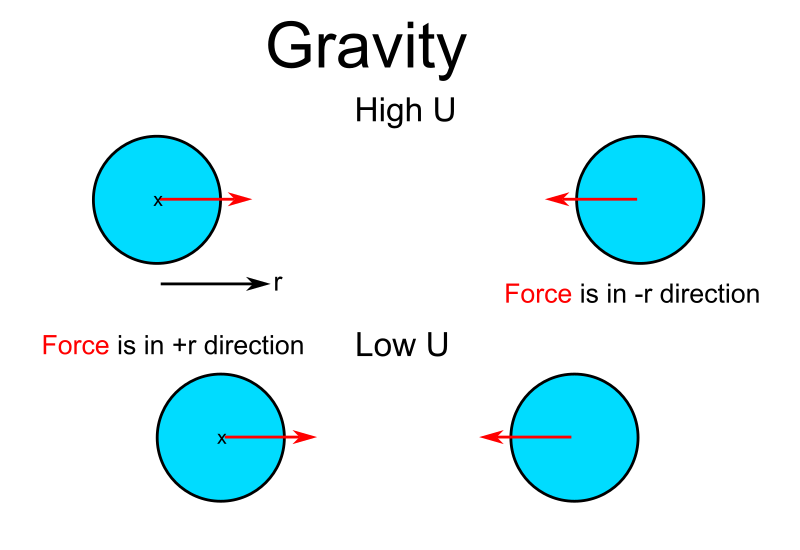
Positive $\hat{r}$ of $\vect{F}_G$ in picture
We must be careful here. In the picture, the origin is on the left ball. The right ball therefore feels a force in the negative $\hat{r}$ direction. The left ball feels an equal but opposite direction force which must therefore be in the positive $\hat{r}$ direction.
However, since the left ball is at the origin, where $r=0$, the calculation of the force would lead to infinity. We therefore use the fact that there is an equal but opposite force to determine the force it feels.
Choosing a positive direction, $U_G=mgh$, and $U_G=-mgh$
$U_G=mgh$ is only if you select up to be positive.
You must use $U_G=-mgh$ if you select down to be positive.
More specifically, if you select the direction where h increases to be the same as the direction where g points (down is positive) then use the negative one.
We can see this from the fact objects want to move from high to low potential energies. Refer to the images for the boxes here.
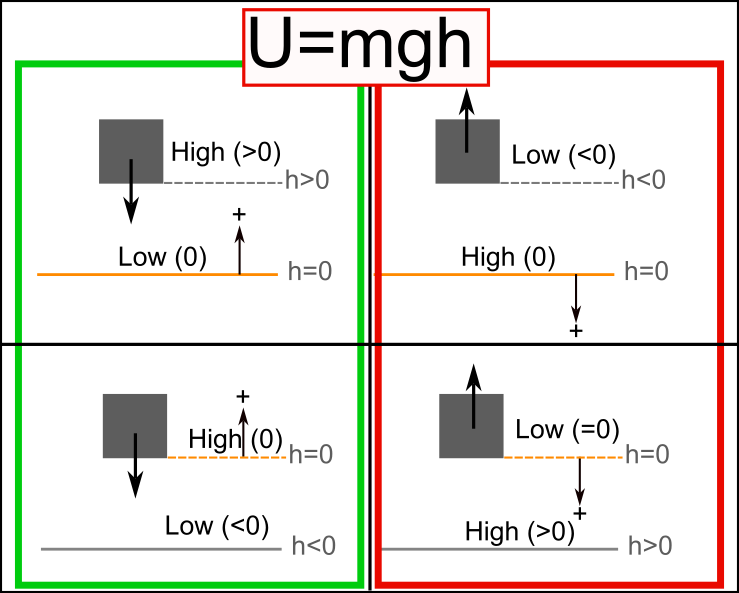
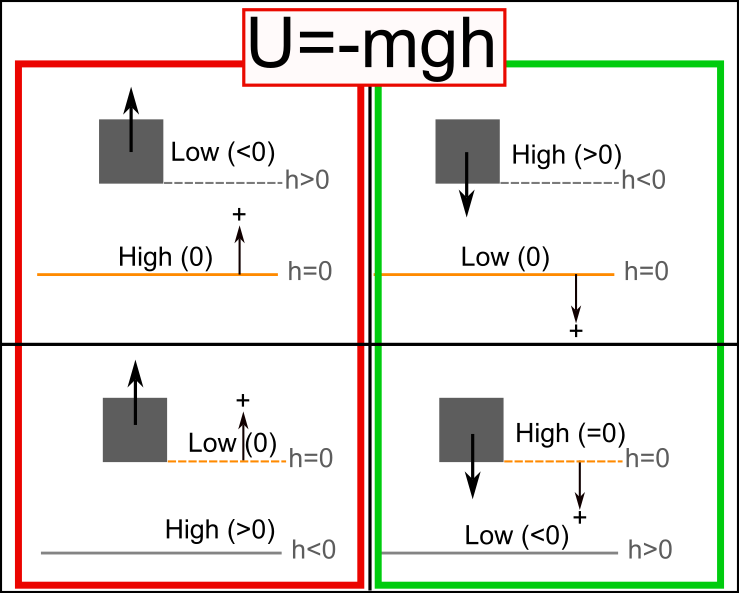
We have four different ways to define positive direction and where the zero is located. We want the box to fall downward in all cases. Only the cases outlined in green give us the box falling toward lower potential energies so those are the only cases we can use. If we wanted to define downward as positive, we would need to use $U=-mgh$ as shown or use $glt0$ which may cause more issues we other familiar equations like the kinematic equations.
Approximation of $U_G$ as mgh
Further explanation is here
The equation $U_G=mgh$ is an approximation that only works when considering a small mass near a much greater mass. If $R$ is the radius of the greater mass object, then the small object must be a distance $h\ll R$ from the surface of the larger object.
For example, the large object is Earth and the small object is a ball 10 cm in diameter. For Earth, $R=6378$ km. In order to use $U=mgh$, the ball cannot be a height $h$ above the surface of Earth close in magnitude to 6378 km. How much less is up to how much error you are willing to have. We can approximate the error by saying that if the ball is at h=600 km, then 600/6000=0.1 is 10% error. Maybe too much. We could restrict to 60 km and have around 1% error.
The international space station orbits around 400 km above the surface so 400/6000=0.0667 is 6.67% error. So we would probably want to use the full equation instead of the approximation for this important project.
